Question

What is the probability a sample of 90 test takers will provide a sample mean test score within 10 points of the population mean of 502 on the Critical Reading part of the test (to 4 decimals)?

Answer 1

0.658 is the probability that a sample 90 test takers will provide a sample mean test score within 10 points of the population mean of 502.

Explanation:

The following information is missing:

The standard deviation of population is 100.

We are given the following information in the question:

Population mean, μ = 502

Standard Deviation, σ = 100

Sample size, n = 90

Standard error =

`(\sigma)/(√(n)) = (100)/(√(90)) = 10.54`

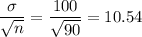
Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

P(test score within 10 points)

`P(492 \leq x \leq 512) \\\\= P(\displaystyle(492 - 502)/(10.54) \leq z \leq \displaystyle(512-502)/(10.54)) \\\\= P(-0.9487 \leq z \leq 0.9487)\\= P(z \leq 0.9487) - P(z < -0.9487)\\= 0.829 -0.171 = 0.658 = 65.8\%`

`P(492 \leq x \leq 512) = 65.8\%`

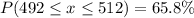
0.658 is the probability that a sample 90 test takers will provide a sample mean test score within 10 points of the population mean of 502.