Question

The endpoints of a diameter of a circle are A(3,1) and B(9,9). Find the area of the circle in terms of pie

Answer 1

The answer is
`25\pi` units squared.

Explanation:

If we find the diameter, we can find the radius by halving the diameter.

We can find the diameter by using the endpoints of the diameter.

The distance formula will give us the length between (3,1) and (9,9).

The distance formula is
`√((x_2-x_1)^2+(y_2-y_1)^2)`.

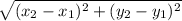The distance between the
`x`'s is 9-3=6.

The distance between the
`y`'s is 9-1=8.

The distance between the points is given by
`√(6^2+8^2)=√(36+64)=√(100)=10`.

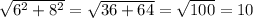The radius is therefore
`(10)/(2)=5`.

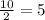We are asked to find the area of this circle.

The formula for finding the area of a circle is
`\pi r^2`.

Since the radius is
`5`, then the area in terms of
`\pi`,(pi), is
`\pi (5)^2=\pi (25)`.

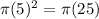The answer is
`25\pi` units squared.