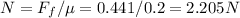Question

A tradesman sharpens a knife by pushing it with a constant force against the rim of a grindstone. The 30-cm-diameter stone is spinning at 200 rpm and has a mass of 28 kg. The coefficient of kinetic friction between the knife and the stone is 0.2. The stone slows steadily to 180 rpm in 10 s of grinding.

a) What is the magnitude of the angular acceleration of the grindstone as it slows down?

b) With what force does the tradesman press the knife against the grindstone?

Answer 1

a. 0.21 rad/s2

b. 2.205 N

Step-by-step explanation:

We convert from rpm to rad/s knowing that each revolution has 2π radians and each minute is 60 seconds

200 rpm = 200 * 2π / 60 = 21 rad/s

180 rpm = 180 * 2π / 60 = 18.85 rad/s

r = d/2 = 30cm / 2 = 15 cm = 0.15 m

a)So if the angular speed decreases steadily (at a constant rate) from 21 rad/s to 18.85 rad/s within 10s then the angular acceleration is

`\alpha = (\Delta \omega)/(\Delta t) = (21 - 18.85)/(10) = 0.21 rad/s^2`

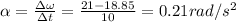
b) Assume the grind stone is a solid disk, its moment of inertia is

`I = mR^2/2`

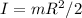
Where m = 28 kg is the disk mass and R = 0.15 m is the radius of the disk.

`I = 28*0.15^2/2 = 0.315 kgm^2`

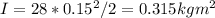
So the friction torque is

`T_f = I\alpha = 0.315*0.21 = 0.06615 Nm`

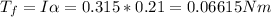
The friction force is

`F_f = T_f/R = 0.06615 / 0.15 = 0.441 N`

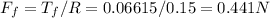
Since the friction coefficient is 0.2, we can calculate the normal force that is used to press the knife against the stone

`N = F_f/\mu = 0.441/0.2 = 2.205 N`