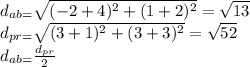Answer:
View graph
Explanation:
Be: p(-3,-1) q(-1,-7) r(3,3)
we must find the value of the middle point a and b
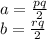
remember that distance between two points is:
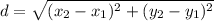
pq=distance between p and q
qr =distance between q and r
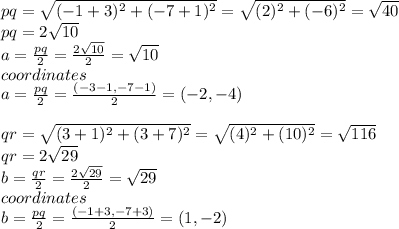
ab is parallel to pr if slope ab is equal to slope pr
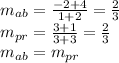
finally distance ab is equal to distance pr/2