Question

to 10 Hz. Superimposed on this signal is 60-Hz noise with an amplitude of 0.1 V. It is desired to attenuate the 60-Hz signal to less than 10% of its value using a Butterworth filter. Select a filter order to perform this task if the corner frequency is 10 Hz.

Answer 1

`G \sqrt{1 +((f)/(f_c))^(2n)} = 1`

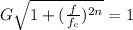
If we square both sides we got:

`G^2 (1+(f)/(f_c))^(2n)= 1`

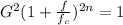
We divide both sides by
`G^2` and we got:

`(1+(f)/(f_c))^(2n) = (1)/(G^2)`

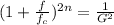
Now we can apply log on both sides and we got:

`2n ln(1+(f)/(f_c)) = ln ((1)/(G^2))`

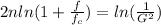
And solving for n we got:

`n = ( ln ((1)/(G^2)))/(2ln(1+(f)/(f_c)))`

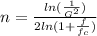
And replacing we got:

`n = (ln ((1)/(0.1^2)))/(2ln(1+(60)/(10)))`

`n = (4.60517)/(3.8918)=1.18`

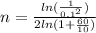
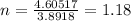
And since n needs to be an integer the correct answer would be n=2 for the filter order.

Step-by-step explanation:

For this case we can use the formula for the Butterworth filter gain given by:

[tec] G = \frac{1}{\sqrt{1 +(\frac{f}{f_c})^{2n}}}[/tex]

Where:

G represent the transfer function and we want that G =0.1 since the desired signal is less than 10% of it's value

`f_c = 10 Hz` represent the corner frequency

`f= 60 Hz` represent the original frequency

n represent the filter order and that's the variable that we need to find

`G \sqrt{1 +((f)/(f_c))^(2n)} = 1`

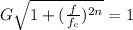
If we square both sides we got:

`G^2 (1+(f)/(f_c))^(2n)= 1`

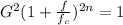
We divide both sides by
`G^2` and we got:

`(1+(f)/(f_c))^(2n) = (1)/(G^2)`

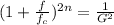
Now we can apply log on both sides and we got:

`2n ln(1+(f)/(f_c)) = ln ((1)/(G^2))`

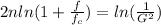
And solving for n we got:

`n = ( ln ((1)/(G^2)))/(2ln(1+(f)/(f_c)))`

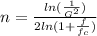
And replacing we got:

`n = (ln ((1)/(0.1^2)))/(2ln(1+(60)/(10)))`

`n = (4.60517)/(3.8918)=1.18`

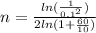
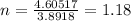
And since n needs to be an integer the correct answer would be n=2 for the filter order.