Question

Please help me! No one has answered me all night and I'm in quite of a bind.

Answer 1

Question # 1

Answer:

Therefore, the vertex form is:

`f(x)=15(x^2+2)^2-79`

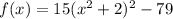
And the vertex of the function is: (-2, -79)

Explanation:

Given the function

`f\left(x\right)=15x^2+60x-19`

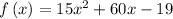
Factoring 15

`f\left(x\right)=15\left(x^2+4x\right)-19`

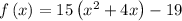
Adding and subtracting the square of half the coefficient of
`x`.

`f\left(x\right)=15\left(x^2+4x+4\right)-19-4* 15`

`f\left(x\right)=15\left(x^2+4x+4\right)-19-60`

`f\left(x\right)=15\left(x^2+2\right)^2-79`

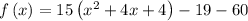
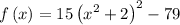
Therefore, the vertex form is:

`f(x)=15(x^2+2)^2-79`

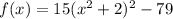
And the vertex of the function is: (-2, -79)

Question # 2

Answer:

• 
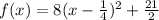  `f(x)=8(x-(1)/(4))^2 +(21)/(2)` is the vertex form of
  `f(x)=8x^2-4x+11`.

Explanation:

Given the function

`f(x)=8x^2-4x+11`

Factoring 8 from the first two terms

`f\left(x\right)=8\left(x^2-(1)/(2)\:x\right)+11`

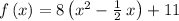
Next adding and subtracting the square of half the coefficient of the linear term

`f\left(x\right)=8\left(x^2-(1)/(2)\:x+(1)/(16)\:\right)+11-8* (1)/(16)`

`f\left(x\right)=8\left(x^2-(1)/(2)\:x+(1)/(16)\:\right)+11-\:(1)/(2)`

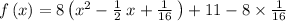
Factoring the perfect square trinomial

`f\left(x\right)=8\left(x-(1)/(4)\right)^2\:+(21)/(2)`

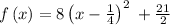
Therefore,

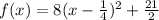`f(x)=8(x-(1)/(4))^2 +(21)/(2)` is the vertex form of
`f(x)=8x^2-4x+11`.