Answer:
Population standard deviation,
 = 3683.063 .
= 3683.063 .
Explanation:
We are given that the width of the estimated confidence interval i.e. 99% is 600 and the sample size used in estimating the mean is 1000 which means ; n = 1000 and width = 600
We know that Width of confidence interval = 2 * Margin of error
Margin of error =
 = 2.5758 *
= 2.5758 *
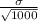 {because at 1% significance level
{because at 1% significance level
z table has value of 2.5758 .}
Therefore, 600 = 2 * 2.5758 *
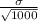
⇒
 =
=
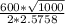 = 3683.063 .
= 3683.063 .
Hence, the Population standard deviation = 3683.063 .