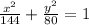Answer:
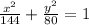
Explanation:
We want to find the equation of an ellipse with foci at (8,0) and (-8,0) and a vertex at (12,0)
This is a horizontal ellipse with its center at the origin.
The equation is of the form:
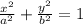
Since the vertex is at (0,12)------>a=12
Since the foci is at
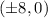 , we have c=8
, we have c=8
Using
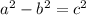
We have
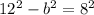
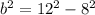
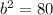
Our equation now becomes:
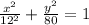
Or