Question

The diameter of bearingsis known to have a mean of 35 mm with a standard deviation of 0.5 mm. A random sample of 36 bearings is selected. What is the probability that the average diameter of these selected bearings will be between 34.95 and 35.18 mm?

Answer 1

Step-by-step explanation:

given,

Mean,μ= 35mm

Standard Deviation,σ = 0.5mm

Sample size, n = 36

Sample Standard deviation =
`(\sigma)/(√(n))`

=
`(0.5)/(6)`

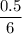
= 0.0833

The interested diameter is between 34.95 to 35.18 mm

Calculating the Z score of the for the diameter mentioned.

`P((x_1-\mu)/(\sigma))<Z<(x_2-\mu)/(\sigma)`

`P((34.95-35)/(0.0833))<Z<(35.18-35)/(0.0833)`

`-0.6< Z < 2.16`

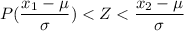
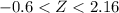
now, Form Z-table

`P(Z<-0.6) = 0.2741`

`P(Z<2.16) = 0.9846`

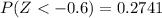
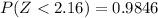
Subtracting the value

= 0.9846 - 0.2741

= 0.71

Hence, the required probability is that the diameter of bearing is in between 34.95 and 35.18 mm is equal to 0.71.