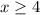Question

What is the piecewise model of f(x)=.7|x-4|+2?

Answer 1

The piecewise model of the function is

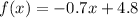`f(x)=-0.7x+4.8` -----> For
`x<4`

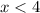
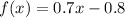`f(x)=0.7x-0.8` -------> For
`x\geq 4`

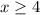
Explanation:

we know that

The general form of absolute value equation is

`f\left(x\right)=a\left|x-h\right|+k`

where

The variable a, tells us how far the graph stretches vertically, and whether the graph opens up or down

(h,k) is the vertex of the absolute value

In this problem we have

`f\left(x\right)=0.7\left|x-4\right|+2`

we have

`a=0.7`

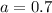
The coefficient a is positive ----> the graphs open up

The vertex is the point (4,2)

Find the piecewise model

case 1) positive value

`f(x)=0.7[(x-4)]+2`

`f(x)=0.7x-2.8+2\\f(x)=0.7x-0.8`

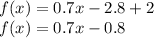
Is a linear equation with positive slope

`(x-4)\geq 0\\x\geq 4`

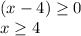
The domain is the interval [4,∞)

case 2) negative value

`f(x)=0.7[-(x-4)]+2`

`f(x)=-0.7x+2.8+2\\f(x)=-0.7x+4.8`

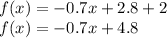
Is a linear equation with negative slope

`(x-4)< 0\\x<4`

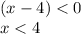
The domain is the interval (-∞,4)

`x<4`

therefore

The piecewise model of the function is

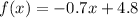`f(x)=-0.7x+4.8` -----> For
`x<4`

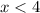
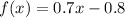`f(x)=0.7x-0.8` -------> For
`x\geq 4`