I need to solve this using l'hopital's rule and logarithmic diferentiation.

Question

asked Feb 6, 2021 45.8k views

1 Answer

Zan · Answer 1 · 2021-02-12T07:59:17+0000

Yo sup??

For our convenience let h=x+1

therefore

when x tends to -1, h tends to 0

hence we can rewrite it as

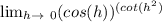
$\lim_(h \to \ 0 ) (cos(h))^((cot(h^2 ))$

This inequality is of the form 1∞

We will now apply the formula

e^(^g^(^x^)^(^f^(^x^)^-^1^)^)

plugging in the values of g(x) and f(x)

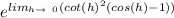
$e^{lim_(h \to \ 0){(cot(h)^2(cos(h)-1))}$

express coth² as cosh²/sinh² and also write cosh-1 as 2sin²(h/2)

(by applying the property that cos2x=1-sin²x)

After this multiply the numerator and denominator with h² so that we can apply the property that

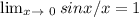
$\lim_(x \to \ 0 ) sinx/x =1$

Now your equation will look like this.

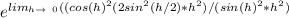
$e^{lim_(h \to \ 0){((cos(h)^2(2sin^2(h/2)*h^2)/(sin(h)^2*h^2)}$

We will now apply the result

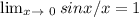
$\lim_(x \to \ 0 ) sinx/x =1$

where x=h²

we get

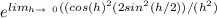
$e^{lim_(h \to \ 0){((cos(h)^2(2sin^2(h/2))/(h^2)}$

we now multiply the numerator and denominator with 4 so that we can say

$\lim_(h^2 \to \ 0 ) sin^2(h/2)/(h^2/4) = 1$

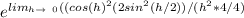
$e^{lim_(h \to \ 0){((cos(h)^2(2sin^2(h/2))/(h^2*4/4)}$

$=e^{lim_(h \to \ 0){((cos(h)^2*2)/(4)}$

Apply the limits and you will get

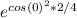
$e^{cos(0)^2*2/4$

=e^(1/2)

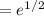
Hope this helps.