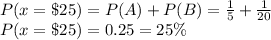Question

Five urns are numbered 3,4,5,6 and 7, respectively. Inside each urn, there are n² dollars where n is the number on the urn.

The following experiment is performed:
An urn is selected at random. If its number is a prime number the experimenter receives the amount in the urn and the experiment is over. If its number is not a prime number, a second urn is selected from the remaining four and the experimenter receives the total amount in the two urns selected.
What is the probability that the experimenter ends up with exactly twenty- five dollars?

Answer 1

0.25 or 25%

Explanation:

3, 5 and 7 are prime numbers.

There are two possible outcomes for which the experimenter ends up with exactly twenty-five dollars:

A) Choosing urn 5 (5 x 5 = 25).

`P(A) = (1)/(5)`

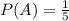
B) Choosing urn 4 and then urn 3 ([4 x 4] + [3 x 3] = 25).

`P(B)= (1)/(5) *(1)/(4)=(1)/(20)`

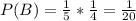
The probability that the experimenter ends up with exactly $25 is:

`P(x=\$25)=P(A)+P(B)= (1)/(5)+(1)/(20)\\P(x=\$25)=0.25=25\%`