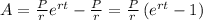Answer:
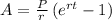
Explanation:
This is a separable differential equation. Rearranging terms in the equation gives
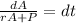
Integration on both sides gives
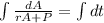
where
 is a constant of integration.
is a constant of integration.
The steps for solving the integral on the right hand side are presented below.
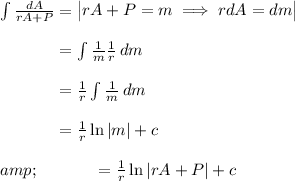
Therefore,

Multiply both sides by
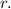
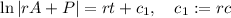
By taking exponents, we obtain
Isolate
 .
.
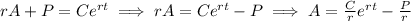
Since
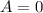 when
when
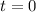 , we obtain an initial condition
, we obtain an initial condition
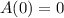 .
.
We can use it to find the numeric value of the constant
 .
.
Substituting
 for
for
 and
and
 in the equation gives
in the equation gives

Therefore, the solution of the given differential equation is