50 points!! Solve |y + 2|>6 A. y<-8 or y>4 B. y<-6 or y>6 C. y

Question

50 points!!

Solve |y + 2|>6

A. y<-8 or y>4

B. y

C. y

Answer 1

`y < -8`

`y > 4`

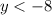
Explanation:

Absolute Value Inequality entered :

|y+2|>6

Step by step solution :
Step 1: Rearrange this Absolute Value Inequality

Absolute value inequalitiy entered

|y+2| > 6

Step 2: Clear the Absolute Value Bars

Clear the absolute-value bars by splitting the equation into its two cases, one for the Positive case and the other for the Negative case.

The Absolute Value term is |y+2|

For the Negative case we'll use -(y+2)

For the Positive case we'll use (y+2)

Step 3: Solve the Negative Case

-(y+2) > 6

Multiply

-y-2 > 6

Rearrange and Add up

-y > 8

Multiply both sides by (-1)

Remember to flip the inequality sign

y < -8

Which is the solution for the Negative Case

Step 4: Solve the Positive Case

(y+2) > 6

Rearrange and Add up

y > 4

Which is the solution for the Positive Case

Step 5:

Wrap up the solution

y < -8

y > 4

Solutions in Interval Notation

(-∞,-8)

(4,+∞)

Solutions on the Number Line

Two solutions were found :

y > 4

y < -8