Answer:
By comparing the ratios of the coefficients, we can determine whether the system has zero,one,or an infinite number of solutions
Explanation:
Here, let us assume the given set of equations is:
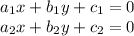
If the system is NOT in above form, convert it in such form.
Now, there are three cases of solution in the given system.
1. The system has NO or ZERO SOLUTION
Consider the given system.
If the ratio
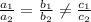
Then the given system of equations has NO SOLUTION.
2. The system has EXACTLY ONE SOLUTION
Consider the given system.
If the ratio
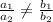
Then the given system of equations has UNIQUE SOLUTION.
3. The system has INFINITELY MANY SOLUTION
Consider the given system.
If the ratio
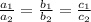
Then the given system of equations has INFINITELY MANY SOLUTION.