
Here, We have given
- 2 squares , In which 1 square is enclosed within the another square and it arranged in a form that it forms 4 right angled triangle
- The height and base of the given right angled triangles are 6 and 3 each.
We know that,
Area of triangle
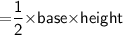
Subsitute the required values,
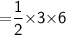
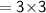
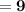
Therefore,
Area covered by 4 right angled triangles

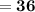
Now,
We have to find the area of the big square
- The length of the side of the big square
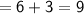
We know that,
Area of square
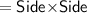
Subsitute the required values,

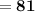
Therefore,
The total area of shaded region
= Area of big square - Area covered by 4 right angled triangle
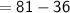
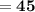
Hence, The total area of shaded region is 45 .
Part 2 :-
Here,
We have to find the area of non shaded region
According to the question
- Hypotenuse = The length of square
Let the hypotenuse of the given right angled triangle be x
Therefore,
By using Pythagoras theorem,
- This theorem states that the sum of the squares of the base and perpendicular height is equal to the square of hypotenuse.
That is,
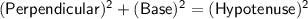
Subsitute the required values
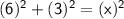
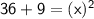
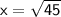
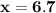
That means,
- The length of the small square = 6.7
We know that ,
Area of square
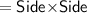
Subsitute the required values,
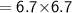
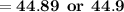
Therefore ,
Area of non shaded region
= Area of big square - Area of small square
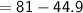

Hence, The total area of non shaded region is 36.1 or 36 (approx) .
Part 3 :-
Here, we have to
- find the total area of the figure
Therefore,
The total area of the figure
= Non shaded region + Shaded region
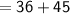
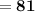
Hence, The total area of the given figure is 81 .