Question

Drag and drop a statement or reason to each box to complete the proof.

Given: parallelogram EFGH

Prove: EG bisects HF and HF bisects EG.

Answer 1

Given Parallelogram EFGH

EG bisects HF and HF bisects EG, if and only if both the diagnols have same mid point.

Explanation:

Step 01:

Let

E be the point (a,b)

F be the point (a',b)

G be the point (a',b')

H be the point (a,b')

Step 02:

Now find mid points of EG and HF

mid point of EG = (
`(a+a')/(2)`,
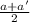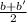`(b+b')/(2)` ) and

mid point of HF = (
`(a'+a)/(2)`,
`(b'+b)/(2)` )

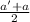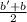Since addition is commutative, and they have the same mid-point, so they bisect each other.

Answer 2

Given : EFGH is a Parallelogram

Prove : EG Bisects HF , HF Bisects EG

Explanation:

Proof

Check image below