Question

Calculate the linear momentum per photon, energy per photon, and the energy per mole of photons for radiation of wavelength for 600 nm (red).

Answer 1

Step-by-step explanation:

It is known that formula for momentum per photon is as follows.

p =
`(h)/(\lambda)`

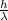
where,
`\lambda` is the photon's wavelength.

Putting the given values into the above formula as follows.

p =
`6.626 * 10^(-34) Joule seconds}{600 * 10^(-9)}m`

=
`1.10 * 10^(-27) kg ms^(-1)`

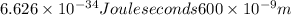
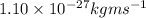
Therefore, the value of linear momentum is
`1.10 * 10^(-27) kg ms^(-1)` .

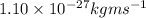Now, energy per photon is calculated as follows.

E =
`(hc)/(\lambda)`

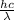
where, h = Planck's constant (
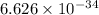`6.626 * 10^(-34)` Joule seconds),

c = the velocity of light (
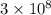`3 * 10^(8)` m/s).

Hence, calculate the energy as follows.

E =
`(hc)/(\lambda)`

=
`6.626 * 10^(-34) Joule seconds * 3 * 10^(8) m/s}{600 * 10^(-9) m`

=
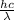
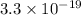`3.3 * 10^(-19)` J

Hence, the value of energy per photon is
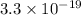`3.3 * 10^(-19)` J.

Now, we will calculate the energy per mole of photons as follows.

E =
`(Nhc)/(\lambda)`

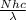
where, E = the energy in a mole of photons,

N = Avogadro's number (
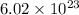`6.02 * 10^(23)` photons per mole),

h = Planck's constant (
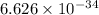`6.626 * 10^(-34)` Joule seconds),

c = the velocity of light (
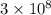`3 * 10^(8)` m/s)

Putting these given values into the above formula and calculate the energy per mole of photons as follows.

E =
`(Nhc)/(\lambda)`

=
`(6.02 * 10^(23) * 6.626 * 10^(-34) * 3 * 10^(8))/(600 * 10^(-9))`

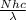
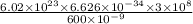
= 199 kJ/mol

Therefore, energy per mole of photons for radiation of wavelength for 600 nm (red) is 199 kJ/mol.