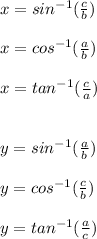Question

Which equations for the measures of the unknown

angles x and y are correct? Check all that apply.
x = costa
x= sin" E)
x= tan'a
y= sin "(a)
y = cos-'

Answer 1

b.) x = sin–1 (c Over b)

c.) x = tan–1 (c Over a)

e.) y = cos–1 (c Over b)

Explanation:

Which equations for the measures of the unknown angles x and y are correct? Check all that apply.

a.) x = cos–1 (a Over c)

b.) x = sin–1 (c Over b)

c.) x = tan–1 (c Over a)

d.) y = sin–1 (a Over c)

e.) y = cos–1 (c Over b)

Sine opposite over hypotenuse

Cosine adjacent over hypotenuse

Tangent opposite over adjacent

SohCahToa this is extremely helpful if you remember that order

Answer 2

Answer: Option B, Option C, Option E

Explanation:

The options written correctly, are:

`A)x = cos^(-1)((a)/(c))\\\\B) x = sin^(-1)((c)/(b))\\\\C)x = tan^(-1)((c)/(a))\\\\D) y = sin^(-1)((a)/(c))\\\\ E)y = cos^(-1)((c)/(b))`

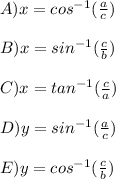
For this exercise you need to use the following Inverse Trigonometric Functions:

`1)\ sin^(-1)(x)\\\\2)\ cos^(-1)(x)\\\\3)\ tan^(-1)(x)\\\\`

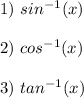
When you have a Right triangle (a triangle that has an angle that measures 90 degrees) and you know that lenght of two sides, you can use the Inverse Trigonometric Functions to find the measure of an angle
`\alpha`:

`1)\alpha = sin^(-1)((opposite)/(hypotenuse)) \\\\2)\ \alpha =cos^(-1)((adjacent)/(hypotenuse))\\\\3)\ \alpha=tan^(-1)((opposite)/(adjacent))`

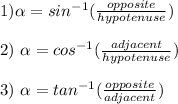
Therefore, the conclusion is that the angles "x" and "y" can be found with these equations:

`x=sin^(-1)((c)/(b))\\\\x= cos^(-1)((a)/(b))\\\\x=tan^(-1)((c)/(a))\\\\\\ y=sin^(-1)((a)/(b))\\\\y=cos^(-1)((c)/(b))\\\\y=tan^(-1)((a)/(c))`