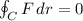Answer:
Explanation:
In this problem, we have a vector field
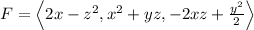 .
.
We need to find the line integral
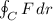
where
 is a circle
is a circle
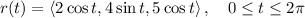 .
.
As we can see, the vector filed
 is defined
is defined
 and its component functions have continuous partial derivatives.
and its component functions have continuous partial derivatives.
First, we need to find the curl of the vector filed
 .
.
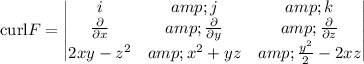
Therefore,
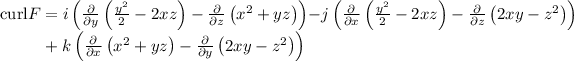
Now, we can easily calculate the needed partial derivatives and we obtain

So, the vector field
 is defined
is defined
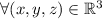 , its component functions have continuous partial derivatives and
, its component functions have continuous partial derivatives and
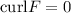 .Therefore, by a well-known theorem,
.Therefore, by a well-known theorem,
 is a conservative field.
is a conservative field.
Since
 is a closed path, we obtain that
is a closed path, we obtain that