Question

Oil Tankers The mean number of oil tankers at a port city is eight per day. Find the probability that the number of oil tankers on any given day is (a) exactly eight, (b) at most three, and (c) more than eight.

Answer 1

a) P(8) = 0.1395

b) P(at most three) = 0.0423684

c) P(X > 8) = 0.41

Explanation:

Data provided in the question:

Mean, μ = 8

Now,

Probability that the number of oil tankers on any given day is

a) exactly eight

using Poisson distribution

we have

P(x) =
`(\mu^xe^(-\mu))/(x!)`

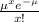
for x = 8

P(8) =
`(8^8e^(-8))/(8!)`

or

P(8) =
`(16777216* e^(-8))/(40320)`

or

P(8) = 0.1395

b) at most three

i.e P(0) + P(1) + P(2) + P(3)

thus,

P(0) =
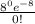`(8^0e^(-8))/(0!)` = 0.0003354

P(1) =
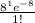`(8^1e^(-8))/(1!)` = 0.002683

P(2) =
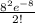`(8^2e^(-8))/(2!)` = 0.01073

P(3) =
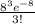`(8^3e^(-8))/(3!)` = 0.02862

⇒ P(at most three) = 0.0003354 + 0.002683 + 0.01073 + 0.02862

= 0.0423684

c) more than eight.

P(X > 8) = 1 - P(X ≤ 8)

Now,

P(0) =
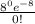`(8^0e^(-8))/(0!)` = 0.0003354

P(1) =
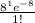`(8^1e^(-8))/(1!)` = 0.002683

P(2) =
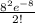`(8^2e^(-8))/(2!)` = 0.01073

P(3) =
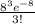`(8^3e^(-8))/(3!)` = 0.02862

P(4) =
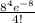`(8^4e^(-8))/(4!)` = 0.05725

P(5) =
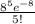`(8^5e^(-8))/(5!)` = 0.091603

P(6) =
`(8^6e^(-8))/(6!)` = 0.1221

P(7) =
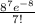`(8^7e^(-8))/(7!)` = 0.13958

P(8) =
`(8^8e^(-8))/(8!)` = 0.13758

Thus,

P(X > 8) = 1 - [ 0.0003354 + 0.002683 + 0.01073 + 0.02862 + 0.05725 + 0.091603 + 0.1221 + 0.13958 + 0.13758 ]

P(X > 8) = 1 - 0.5904814

or

P(X > 8) = 0.41