Question

A sandwich shop makes fresh sandwiches every morning, before opening. The average underage cost is $3.00 per sandwich, and the average overage cost is $5.60 per sandwich. Based on past data, the number of sandwiches sold on a single day is normally distributed, with a mean of 52.1 sandwiches and a standard deviation of 7.8. How many sandwiches should the store make every morning, in order to maximize its expected profit?

Group of answer choices 
A. 59
B. 44
C. 52
D. 49

Answer 1

Option (D) 49

Step-by-step explanation:

Data provided in the question:

Average underage cost,
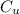`C_u` = $3.00 per sandwich

Average overage cost
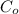`C_o` = $5.60 per sandwich

Mean = 52.1 sandwich

Standard deviation = 7.8

Now,

Critical ratio,
`C_R` =
`(C_u)/(C_u+C_o)`

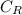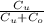
= 3 ÷ [ 3 + 5.6 ]

= 0.3488

Z value for Critical ratio = -0.389 [ From standard z value table ]

Therefore,

Order quantity to maximize profit

= Mean + Z × Standard deviation

= 52.1 + [ -0.389 × 7.8 ]

= 49

Hence,

Option (D) 49