Question

The compass in a plane indicates that it is headed due east. Its airspeed moniotor indicates that the speed of the plane with respect to the air is ~vP/A = 215 km/h. A steady wind of 65.0 km/h is blowing due north.

a. What is the velocity of the plane with respect to the ground?
b. If the pilot wishes to fly due east, what must be the heading?

Answer 1

given,

speed of plane in east, v_e = 215 Km/hr

speed of wind in north, v_w = 65 Km/hr

a) velocity of plane w.r.t. to ground

resultant of the velocity

`V =√(v_e^2 +v_w^2)`

`V =√(215^2 +65^2)`

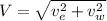
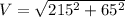
V = 225 Km/h (approximately)

angle w.r.t to ground

`\theta = tan^(-1)(v_w)/(v_e)`

`\theta = tan^(-1)(65)/(215)`

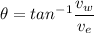
θ = 16.82°

b) if driver want to head east

angle,

`\theta = sin^(-1)(v_w)/(v_e)`

`\theta = sin^(-1)(65)/(215)`

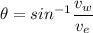
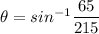
θ = 17.6°

velocity would be equal to

v = v_e cos θ

v = 215 cos 17.6°

v = 205 Km/h