Question

If a = 6, −9, 3 , then what is 4a?

4a = How does the magnitude of 4a compare to the magnitude of a?
1. The magnitude of 4a is the same as the magnitude of a.
2. The magnitude of 4a is a factor of 4 greater than the magnitude of a.
3. The magnitude of 4a is zero.
4. The magnitude of 4a is a factor of 4 less than the magnitude of a.
5. Not enough information is given.

Answer 1

Option 2.

Explanation:

It is given that

a = <6,-9,3>

We need to compare the maginitude of vertor a and vector 4a.

If a vector is defined as v = <x,y,z>, then its magnitude is defined as

`|v|=√(x^2+y^2+z^2)`

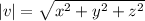
Using the above formula we get

`|a|=√(6^2+(-9)^2+(3)^2)`

`|a|=√(126)`

`|a|=√(9* 14)`

`|a|=3√(14)`

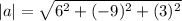
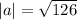
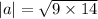
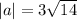
The vector 4a is

`4a=<4(6),4(-9),4(3)>=<24,-36,12>`

`|4a|=√((24)^2+(-36)^2+(12)^2)`

`|4a|=√(4^2(6^2+(-9)^2+(3)^2))`

`|4a|=4√(6^2+(-9)^2+(3)^2)`

`|4a|=4|a|`

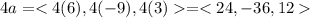
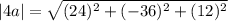
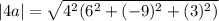
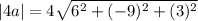
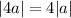
The magnitude of 4a is a factor of 4 greater than the magnitude of a.

Therefore, the correct option is 2.