Question

the speed of a stream is 4mph. If a boat travels 92 miles downstream in the same time that it takes to travel 46 miles upstream, what is the speed of the boat in still water?

Answer 1

12 miles per hour

Explanation:

Let speed of boat in still water be "x"

and speed of current be "c"

So, downstream rate would be "x + c"

And, upstream rate would be "x - c"

Now, given c = 4

We can use the distance formula, D = RT, where

D is distance, R is rate, and T is time

to solve this.

Downstream:

D = RT

92 = (x+4)(t)

Upstream:

D = RT

46 = (x-4)(t)

Both the times are same, we can equate both the times. Lets simplify first:

t = 92/(x+4)

and

t = 46/(x-4)

Equate:

`(92)/(x+4)=(46)/(x-4)`

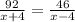
Now, cross multiply and solve for x to get our answer:

`(92)/(x+4)=(46)/(x-4)\\92(x-4)=46(x+4)\\92x-368=46x+184\\46x=552\\x=12`

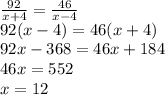
Speed of Boat (in still water) = 12 mph