Answer:
The amount of the chemical flows into the tank during the firs 20 minutes is 4200 liters.
Explanation:
Consider the provided information.
A chemical flows into a storage tank at a rate of (180+3t) liters per minute,
Let
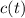 is the amount of chemical in the take at t time.
is the amount of chemical in the take at t time.
Now find the rate of change of chemical flow during the first 20 minutes.
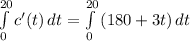
![\int\limits^(20)_(0) {c'(t)} \, dt =\left[180t+(3)/(2)t^2\right]^(20)_0](https://img.qammunity.org/2021/formulas/mathematics/high-school/jhbnkrk6zxi0vighetpkgk0jc3h3ju3s4j.png)


So, the amount of the chemical flows into the tank during the firs 20 minutes is 4200 liters.