Answer:
The instantaneous voltage (
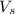 ) across the half-wave rectifier is given by
) across the half-wave rectifier is given by
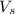 (t) =
(t) =
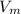 cos(wt + θ) V ------------ (i)
cos(wt + θ) V ------------ (i)
Where
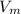 is the peak voltage and Θ is the phase angle.
is the peak voltage and Θ is the phase angle.
Given:
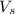 (t) = 170sin(377t) V -------------------------(ii)
(t) = 170sin(377t) V -------------------------(ii)
Load Resistance R = 15Ω
Comparing equations (i) and (ii)
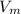 = 170V
= 170V
(a) Average load current
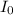 =
=
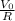 =
=
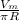
Taking pi as 22/7 and substituting the values of R and
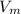 into the above equation, we have;
into the above equation, we have;
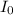 =
=
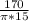 = 3.6A
= 3.6A
(b) The rms load current
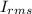 =
=
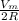
Substituting the values of R and
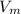 into the equation above gives;
into the equation above gives;
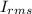 =
=
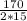 = 5.67A
= 5.67A
(c). Power absorbed by the load is given by the ac and the dc.
Dc Power absorbed =
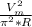 =
=
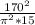 = 195W
= 195W
Ac Power absorbed =
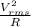
where
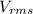 =
=
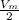 =
=
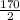 = 85V
= 85V
Therefore, Ac Power absorbed =
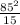 = 481.67W
= 481.67W
(d) Apparent Power is the product of the rms values of the current and the voltage.
Apparent Power =
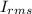 *
*
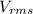
Apparent Power = 5.67 * 85 = 481.95W
(e) Power factor is the ratio of the Power absorbed by load to the Apparent Power
Therefore Power factor =
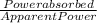
Power factor =
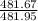 = 0.999
= 0.999
PS: Power absorbed could also be called the real power
Hope this helps