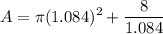Question

A metal cylinder can with an open top and closed bottom is to have volume 4 cubic feet. Approximate the dimensions that require the least amount of material. What would this amount be?

Answer 1

`r\approx 1.084\ feet`

`h\approx 1.084\ feet`

`\displaystyle A=11.07\ ft^2`

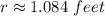
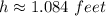
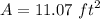
Explanation:

Optimizing With Derivatives

The procedure to optimize a function (find its maximum or minimum) consists in :

• Produce a function which depends on only one variable
• Compute the first derivative and set it equal to 0
• Find the values for the variable, called critical points
• Compute the second derivative
• Evaluate the second derivative in the critical points. If it results positive, the critical point is a minimum, if it's negative, the critical point is a maximum

We know a cylinder has a volume of 4
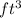`ft^3`. The volume of a cylinder is given by

`\displaystyle V=\pi r^2h`

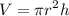
Equating it to 4

`\displaystyle \pi r^2h=4`

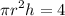
Let's solve for h

`\displaystyle h=(4)/(\pi r^2)`

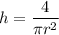
A cylinder with an open-top has only one circle as the shape of the lid and has a lateral area computed as a rectangle of height h and base equal to the length of a circle. Thus, the total area of the material to make the cylinder is

`\displaystyle A=\pi r^2+2\pi rh`

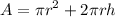
Replacing the formula of h

`\displaystyle A=\pi r^2+2\pi r \left ((4)/(\pi r^2)\right )`

Simplifying

`\displaystyle A=\pi r^2+(8)/(r)`

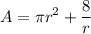
We have the function of the area in terms of one variable. Now we compute the first derivative and equal it to zero

`\displaystyle A'=2\pi r-(8)/(r^2)=0`

Rearranging

`\displaystyle 2\pi r=(8)/(r^2)`

Solving for r

`\displaystyle r^3=(4)/(\pi )`

`\displaystyle r=\sqrt[3]{(4)/(\pi )}\approx 1.084\ feet`

Computing h

`\displaystyle h=(4)/(\pi \ r^2)\approx 1.084\ feet`

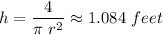
We can see the height and the radius are of the same size. We check if the critical point is a maximum or a minimum by computing the second derivative

`\displaystyle A''=2\pi+(16)/(r^3)`

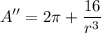
We can see it will be always positive regardless of the value of r (assumed positive too), so the critical point is a minimum.

The minimum area is

`\displaystyle A=\pi(1.084)^2+(8)/(1.084)`

`\boxed{ A=11.07\ ft^2}`