Question

A research company desires to know the mean consumption of meat per week among people over age 40. A sample of 610 people over age 40 was drawn and the mean meat consumption was 3.1 pounds. Assume that the population standard deviation is known to be 1.1 pounds. Construct the 85% confidence interval for the mean consumption of meat among people over age 40. Round your answers to one decimal place.

Answer 1

Answer:
`(3.0,\ 3.2)`

Explanation:

Confidence interval for population mean is given by :-

`\overline{x}\pm z_(\alpha/2)(\sigma)/(√(n))` (1)

, where
`\overline{x}` = Sample mean

`z_(\alpha/2)`= Critical z-value

`\sigma` = Population standard deviation.

n= Sample size.

As per given , we have

n= 610

`\sigma=1.1`

`\overline{x}=3.1`

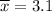
Significance level for 85% confidence :
`\alpha=1-0.85=0.15`

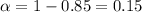
By z-table critical two tailed z-value :
`z_(\alpha/2)=z_(0.075)=1.44`

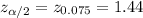
Put all values in (1) , we get

`3.1\pm 1.44(1.1)/(√(610))`

`3.1\pm 1.44(1.1)/(24.698)`

`3.1\pm 0.064`

`=(3.1-0.064,\ 3.1+0.064)=(3.036,\ 3.164)\approx(3.0,\ 3.2)`

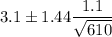
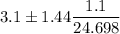
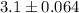
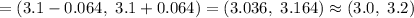
Hence, the 85% confidence interval for the mean consumption of meat among people over age 40. =
`(3.0,\ 3.2)`