Question

Part A: Determine the wavelength of photons that can be emitted

from of the n=4 state of a hydrogen atom to the n=1 state. Give
answer in nm .
Part B: determine the wavelength of photons that can it be
emitted from of the n=4 state of a hydrogen atom to the n=2
state. Give answer in nm .
Part C: Determine the wavelength of photons that can be
emitted from of the n=4 state of a hydrogen atom to the n=3 state.
Give answer in nm .

Answer 1

A λ = 97.23 nm

, B) λ = 486.2 nm

, C) λ = 53326 nm

Step-by-step explanation:

With that problem let's use the Bohr model equation for the hydrogen atom

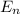`E_(n)` = -k e² /2a₀ 1/n²

For a transition between two states we have

`E_(nf)` -
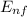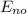`E_(no)` = -k e² /2a₀ (1/
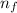`n_(f)`² - 1 / n₀²)

Now this energy is given by the Planck equation

E = h f

And the speed of light is

c = λ f

Let's replace

h c / λ = - k e² /2a₀ (1 /
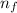`n_(f)`² - 1 / no₀²)

1 / λ = - k e² /2a₀ hc (1 /
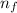`n_(f)`² -1 / n₀²)

Where the constants are the Rydberg constant
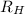`R_(H)` = 1.097 10⁷ m⁻¹

1 / λ =
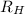`R_(H)` (1 / n₀² - 1 / nf²)

Now we can substitute the given values

Part A

Initial state n₀ = 1 to the final state
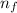`n_(f)` = 4

1 / λ = 1.097 10⁷ (1/1 - 1/4²)

1 / λ = 1.0284 10⁷ m⁻¹

λ = 9.723 10⁻⁸ m

We reduce to nm

λ = 9.723 10⁻⁸ m (10⁹ nm / 1m)

λ = 97.23 nm

Part B

Initial state n₀ = 2 final state
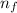`n_(f)` = 4

1 / λ = 1.097 10⁷ (1/2² - 1/4²)

1 / λ = 0.2056 10⁻⁷ m

λ = 486.2 nm

Part C

Initial state n₀ = 3

1 / λ = 1,097 10⁷ (1/3² - 1/4²)

1 / λ = 5.3326 10⁵ m⁻¹

λ = 5.3326 10-5 m

λ = 53326 nm