Answer:
36 feet.
Explanation:
We have been given that a ball is thrown upward from ground level. Its height h, in feet, above the ground after t seconds is
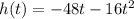 . We are asked to find the maximum height of the ball.
. We are asked to find the maximum height of the ball.
We can see that our given equation is a downward opening parabola, so its maximum height will be the vertex of the parabola.
To find the maximum height of the ball, we need to find y-coordinate of vertex of parabola.
Let us find x-coordinate of parabola using formula
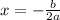 .
.
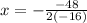
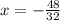
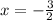
So, the x-coordinate of the parabola is
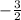 . Now, we will substitute
. Now, we will substitute
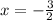 in our given equation to find y-coordinate of parabola.
in our given equation to find y-coordinate of parabola.
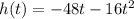
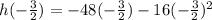
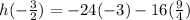
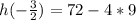
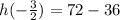

Therefore, the maximum height of the ball is 36 feet.