Answer:
c. standard deviation, median, range
Explanation:
The standard deviation without the Bessel's correct is defined as:
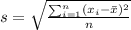
And if we find the expected value for s we got:

![E(s^2)= (1)/(n) E[\sum_(i=1)^n ((x_i -\mu)-(\bar x -\mu)^2)]](https://img.qammunity.org/2021/formulas/mathematics/college/k3dcy27fjgu39iosrglq38q8bb7z8cwapn.png)
We have this:
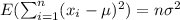
![E[\sum_(i=1)^n (x_i -\mu)(\bar x -\mu)]= \sigma^2](https://img.qammunity.org/2021/formulas/mathematics/college/i0231znuz3fmml219qai4rldaedqradlb5.png)
![E[\sum_(i=1)^n (\bar x -\mu)^2]=\sigma^2](https://img.qammunity.org/2021/formulas/mathematics/college/alhx1w0ekughln2grpj2n3ntvai0kx5ubl.png)
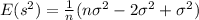
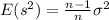
as we can see the sample variance is a biased estimator since:

And we see that the standard deviation is biased, since:
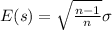
because
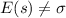
The mean is not biased for this case option a is FALSE.
The proportion is not biased for this reason option d is FALSE
The range can be considered as biased since we don't have info to conclude that the range follows a distirbution in specific.
The sample median "is an unbiased estimator of the population median when the population is normal. However, for a general population it is not true that the sample median is an unbiased estimator of the population median".
And for this reason the best option is c.