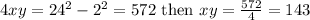If the sum of two positive integers is 24 and the difference of their squares is 48, what is the product of the two integers?(A) 108(B) 119(C) 128(D) 135(E) 143

Question

asked Mar 3, 2021 4.2k views

1 Answer

Gil Margolin · Answer 1 · 2021-03-09T19:22:56+0000

Answer:

143

Explanation:

Denote by x and y such integers. The hypotheses given can be written as:

x+y=24, x^2-y^2=48

Use the difference of squares factorization to solve for x-y

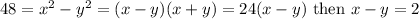
$48=x^2-y^2=(x-y)(x+y)=24(x-y)\text{ then }x-y=2$

Remember that

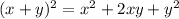
(x+y)^2=x^2+2xy+y^2

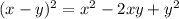
(x-y)^2=x^2-2xy+y^2

Substract the second equation from the first to obtain

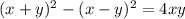
(x+y)^2-(x-y)^2=4xy

Substituting the known values, we get

$4xy=24^2-2^2=572\text{ then }xy=(572)/(4)=143$