Since the unit circle has a radius of 1 we know that r = 1 and that our angle is 60 degrees. Using sin and cos functions we can then find the x and y coordinates of point A. since
 and
and
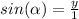 (where
(where
 = the angle)
= the angle)
 because of the identity that cos(a) = x and sin(a) = y
because of the identity that cos(a) = x and sin(a) = y
Using the angle and the previously described identity we can find the coordinates with cos(60) = x = 1/2 and sin(60) = y =
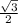 to get A =(x,y) =
to get A =(x,y) =
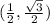 .
.
From here we can work backwards and find that BC = x =
 and that AC = y =
and that AC = y =
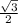 and finally we know that AB = r = 1 because it is a radius of the unit circle and must be 1.
and finally we know that AB = r = 1 because it is a radius of the unit circle and must be 1.
-This probably isn't the way you were taught to solve this problem, but it is how we do it in physics and real-life.