Answer:
1. x = -1
2. y = -1, y = 2
3. y = -½ + i
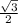 ; y = -½ - i
; y = -½ - i
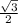
4. x = -3; x = -6
Explanation:
I will only produce work for questions 1 through 4, and you could follow the same steps for questions 5 and 6 so that you could learn and get used to solving quadratic equations. I am practically using the same techniques in solving questions 1 through 4 anyway.
1.) x² + 2x + 1 = 0
where a = 1, b = 2, c = 1
Determine the nature and number of solutions based on the discriminant, b² - 4ac:
b² - 4ac = 2² - 4(1)(1) = 4 - 4 = 0
This means that the equation has one real root.
Next, determine the factors of the quadratic equation.
Use the perfect square trinomial factoring technique:
u² + 2uv + v² = (u + v)²
From the equation, x² + 2x + 1 = 0
where a = 1, b = 2, c = 1
Find factors with product a × c and sum b:
Possible factors:
product a × c : 1 × 1 = 1
sum b : 1 + 1 = 2
Therefore, the binomial factors of x² + 2x + 1 = 0 is (x + 1)²
To find the roots, set x = 0:
x + 1 = 0
Subtract 1 from both sides to isolate x:
x + 1 - 1 = 0 - 1
x = -1 (This is the root of the equation).
2) y² - y - 2 = 0
where a = 1, b = -1, and c = -2
Determine the nature and number of solutions based on the discriminant, b² - 4ac:
b² - 4ac = (-1)² - 4(1)(-2) = 9
Since b² - 4ac > 0, then it means that the equation will have two real roots.
From the equation, y² - y - 2 = 0
where a = 1, b = -1, and c = -2:
Find factors with product a × c and sum b:
Product a × c :
1 × -2 = -2
-1 × 2 = -2
Sum b:
1+ (-2) = -1
-1 + 2 = 1
Therefore, the possible factors are: 1 and -2:
(y + 1) (y - 2)
To find the roots, set y = 0:
y + 1 = 0
Subtract 1 from both sides:
y + 1 - 1 = 0 - 1
y = -1
y - 2 = 0
Add 2 to both sides:
y -2 + 2 = 0 + 2
y = 2
Therefore, the roots of the quadratic equation, y² - y - 2 = 0 are: y = -1 and y = 2.
3.) y² + y + 1 = 0
where a = 1, b = 1, and c = 1
Determine the nature and number of solutions based on the discriminant, b² - 4ac:
b² - 4ac = (1)2 - 4(1)(1) = -3
Since b² - 4ac < 0, then it means that the equation will have two complex roots.
Use the Quadratic Formula:
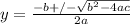
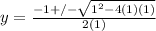
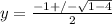
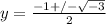
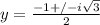
Therefore, the roots of the quadratic equation, y² + y + 1 = 0 are:
y = -½ + i
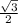 ; y = -½ - i
; y = -½ - i
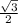
4) x² + 9x + 18 = 0
where a = 1, b = 9, and c = 18.
Determine the nature and number of solutions based on the discriminant, b² - 4ac:
b² - 4ac = (9)2 - 4(1)(18) = 9
Since b² - 4ac > 0, then it means that the equation will have two real roots.
Use the Quadratic Formula:
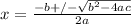

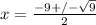
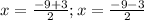
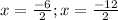
x = -3; x = -6
Therefore, the roots of the quadratic equation, x² + 9x + 18 = 0
are: x = -3 and x = -6.