We're given the vectors

(a) Two vectors are perpendicular if their dot product is zero. For instance,
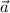 and
and
 are not perpendicular because
are not perpendicular because
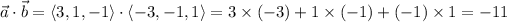
You'll find that none of these vectors taken two at a time are perpendicular to each other.
(b) Recall for any two vectors
 and
and
 that
that
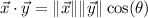
where
 is the angle between
is the angle between
 and
and
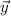 . If these vectors are parallel, then the angle between them is 0 rad or π rad, meaning they point in the same or in opposite directions, respectively.
. If these vectors are parallel, then the angle between them is 0 rad or π rad, meaning they point in the same or in opposite directions, respectively.
We have cos(0) = 1 and cos(π) = -1, so
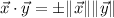
For instance, we know that
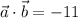
and we have
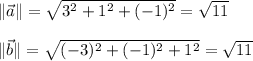
so
 and
and
 are indeed parallel and point in opposite directions, since -11 = - √11 × √11.
are indeed parallel and point in opposite directions, since -11 = - √11 × √11.
On the other hand,
 and
and
 are not parallel, since
are not parallel, since
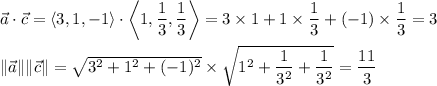
and clearly 3 ≠ ±11/3.
It turns out that (a, b) is the only pair of parallel vectors.
(c) The cosine of an angle measuring between 0 and π/2 rad is positive, so you just need to check the sign of

For instance, we know
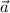 and
and
 are parallel and have an angle of π rad between them. cos(π) = -1, so this pair doesn't qualify. Meanwhile, the angle between
are parallel and have an angle of π rad between them. cos(π) = -1, so this pair doesn't qualify. Meanwhile, the angle between
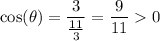
so
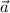 and
and
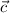 do qualify.
do qualify.
You'd find that the pairs ((a, c), (a, d), (a, g), (c, d), (c, g), (d, g)).
(d) An angle between π/2 and π has a negative cosine. None of the vectors are perpendicular to each other, so this happens for the remaining pairs, ((a, b), (b, c), (b, d), (b, g)).