- Simplify :- 1 + - w² + 9w.
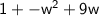
Quadratic polynomial can be factored using the transformation
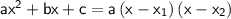 , where
, where
 are the solutions of the quadratic equation
are the solutions of the quadratic equation
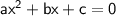 .
.
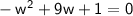
All equations of the form
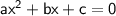 can be solved using the quadratic formula:
can be solved using the quadratic formula:
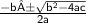 . The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.
. The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.
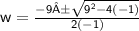
Square 9.
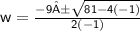
Multiply -4 times -1.
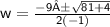
Add 81 to 4.

Multiply 2 times -1.
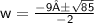
Now solve the equation
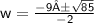 when ± is plus. Add -9 to
when ± is plus. Add -9 to
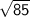 .
.
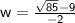
Divide -9+
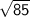 by -2.
by -2.

Now solve the equation
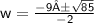 when ± is minus. Subtract
when ± is minus. Subtract
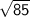 from -9.
from -9.
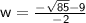
Divide
 by -2.
by -2.
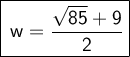
Factor the original expression using
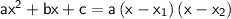 . Substitute
. Substitute
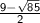 for
for
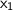 and
and
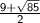 for
for
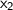 .
.

NOTE :-
Well, in the picture you inserted it says that it's 8th grade mathematics. So, I'm not sure if you have learned simplification with the help of biquadratic formula. So, if you want the answer simplified only according to like terms then your answer will be ⇨

This cannot be further simplified as there are no more like terms (you can use the biquadratic formula if you've learned it.)