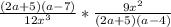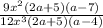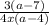Question

Change the following mixed expressions to fractions and then simplify the complex fractions.

Answer 1

I believe the answer would be
3(9-7)
4x(a=4)

Answer 2

`(3(a-7))/(4x(a-4))`

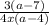
Explanation:

One is given the following expression:

`(2a^2-9a-35)/(12x^3)*(9x^2)/(2a^2-3a-20)`

The most logical first step to solve this equation is to factor it. Rewrite each quadratic equation as the product of two linear equations. Unfortunately, no additional explanation can be provided. To prove that the product of the two linear terms are the factors of the quadratic term, one must distribute and simplify,

`(2a^2-9a-35)/(12x^3)*(9x^2)/(2a^2-3a-20)`

`((2a+5)(a-7))/(12x^3)*(9x^2)/((2a+5)(a-4))`

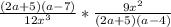
Now simplify this expression, then cancel common terms in the numerator and denominator,

`((2a+5)(a-7))/(12x^3)*(9x^2)/((2a+5)(a-4))`

`(9x^2(2a+5)(a-7))/(12x^3(2a+5)(a-4))`

`(3(a-7))/(4x(a-4))`