Question

Plzz help............​

Answer 1

Answer: Choice A

`(4)/(\pi)\left[x*\sin^(-1)(x)+√(1-x^2)\right]-x+C\\\\`

====================================================

Proof:

Apply the derivative to choice A. The goal is to prove the derivative is equivalent to the given integrand.

`y = (4)/(\pi)\left[x*\sin^(-1)(x)+√(1-x^2)\right]-x+C\\\\(dy)/(dx) = (4)/(\pi)\left[\sin^(-1)(x)+(x)/(√(1-x^2))-(x)/(√(1-x^2))\right]-1\\\\(dy)/(dx) = (4)/(\pi)\sin^(-1)(x)-1\\\\`

It's far from obvious, but we can apply a bit of algebra like so

`(dy)/(dx) = (4)/(\pi)\sin^(-1)(x)-1\\\\(dy)/(dx) = (4)/(\pi)\sin^(-1)(x)-(\pi)/(\pi)\\\\(dy)/(dx) = (4\sin^(-1)(x)-\pi)/(\pi)\\\\`

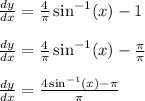
Next, we divide every term by 2. This is so we can replace the pi terms with pi/2

`(dy)/(dx) = (4\sin^(-1)(x)-\pi)/(\pi)\\\\(dy)/(dx) = (2\sin^(-1)(x)-(\pi)/(2))/((\pi)/(2))\\\\`

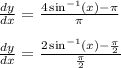
We do this to take advantage of the trig identity
`\sin^(-1)(x)+\cos^(-1)(x) = (\pi)/(2)`

So we'll be replacing every instance of "pi/2" with the left hand side of that equation just mentioned.

Therefore,

`(dy)/(dx) = (2\sin^(-1)(x)-(\pi)/(2))/((\pi)/(2))\\\\(dy)/(dx) = (2\sin^(-1)(x)-\left(\sin^(-1)(x)+\cos^(-1)(x)\right))/(\sin^(-1)(x)+\cos^(-1)(x))\\\\(dy)/(dx) = (2\sin^(-1)(x)-\sin^(-1)(x)-\cos^(-1)(x))/(\sin^(-1)(x)+\cos^(-1)(x))\\\\(dy)/(dx) = (\sin^(-1)(x)-\cos^(-1)(x))/(\sin^(-1)(x)+\cos^(-1)(x))\\\\`

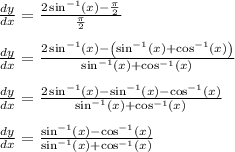
This shows that differentiating the expression in choice A leads to the given integrand.

If we reverse all of the steps mentioned, then we can show that:

`\displaystyle(dy)/(dx) = (\sin^(-1)(x)-\cos^(-1)(x))/(\sin^(-1)(x)+\cos^(-1)(x))\\\\\\ \int(dy)/(dx)dx = \int(\sin^(-1)(x)-\cos^(-1)(x))/(\sin^(-1)(x)+\cos^(-1)(x))dx\\\\\\y = (4)/(\pi)\left[x*\sin^(-1)(x)+√(1-x^2)\right]-x+C\\\\`

since integrals and derivatives are tied together through inverse processes (one undoes the other more or less).