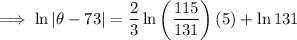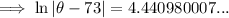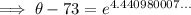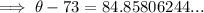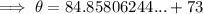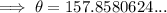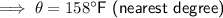Question

After heating up in a teapot, a cup of hot water is poured at a temperature of 204^\circ204

∘
F. The cup sits to cool in a room at a temperature of 73^\circ73
∘
F. Newton's Law of Cooling explains that the temperature of the cup of water will decrease proportionally to the difference between the temperature of the water and the temperature of the room, as given by the formula below:

The cup of water reaches the temperature of 188^\circ188
∘
F after 1.5 minutes. Using this information, find the value of kk, to the nearest thousandth. Use the resulting equation to determine the Fahrenheit temperature of the cup of water, to the nearest degree, after 5 minutes.

Answer 1

158°F (nearest degree)

Explanation:

Solving using Newton's Law of Cooling

Newton's Law of Cooling Formula:

`T(t)=T_S+(T_0-T_S)e^(-kt)`

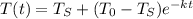
where:

• 
  `t` = time
• 
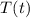  `T(t)` = temperature of the water at time (t)
• 
  `T_S` = surrounding temperature
• 
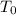  `T_0` = initial temperature of the water
• 
  `k` = constant

Given:

• 
  `T_0=204`
• 
  `T_S=73`
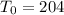
• T(t) = 188 when t = 1.5m

Substituting given values into the formula and solve for k:

`\implies 188=73+(204-73)e^(-1.5k)`

`\implies (115)/(131)=e^(-1.5k)`

`\implies \ln(115)/(131)={-1.5k`

`\implies k=-\frac23\ln(115)/(131)`

`\implies k=0.087 \textsf{ (nearest thousandth)}`

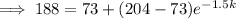
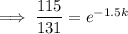
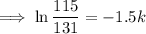
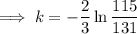
So the final equation is:

`T(t)=73+131e^(-0.087t)`

Therefore, when t = 5:

`73+131e^(-0.087 * 5)=157.7916714...`

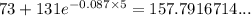
= 158 °F (nearest degree)

Solving using differential equations

The temperature (
`\theta`) of the cup of water will decrease proportionally to the difference between the temperature of the water (
`\theta`) and the temperature of the room (73°F):

`(d\theta)/(dt) \propto(\theta-73)`

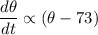
Change this to an equation by introducing a constant k. As the rate of change of temperature is decreasing, we need to introduce a negative sign:

`\implies (d\theta)/(dt)=-k(\theta-73)`

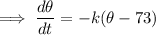
Now solve the differential equation:

`\int\limits {\left((1)/(\theta-73)\right) \, d\theta =\int\limits {(-k)} \, dt`

`\ln|\theta-73|=-kt+C`

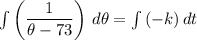
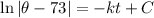
To find the constants k and C, use the given conditions:

• 
  `t=0, \theta=204 \textdegree F`

`\implies \ln|204-73|=-k(0)+C`

`\implies \ln131=C`

`\implies \ln|\theta-73|=-kt+\ln131`

• 
  `t=1.5, \theta=188 \textdegree F`

`\implies \ln|188-73|=-k(1.5)+\ln131`

`\implies \ln115=-1.5k+\ln131`

`\implies \ln115-\ln131=-1.5k`

`\implies -\frac23\ln\left((115)/(131)\right)=k`

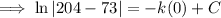
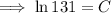
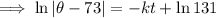
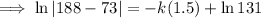
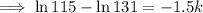
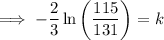
Therefore, final equation:

`\implies \ln|\theta-73|=\frac23\ln\left((115)/(131)\right)t+\ln131`

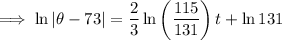
When t = 5:

`\implies \ln|\theta-73|=\frac23\ln\left((115)/(131)\right)(5)+\ln131`

`\implies \ln|\theta-73|=4.440980007...`

`\implies \theta-73=e^(4.440980007...)`

`\implies \theta-73=84.85806244...`

`\implies \theta=84.85806244...+73`

`\implies \theta=157.8580624...`

`\implies \theta=158 \textdegree \textsf{F (nearest degree)}`