Answer:
The sum of the arithmetic series is 2717.
Explanation:
The sum of an arithmetic sequence is given by:
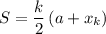
Where k is the number of terms, a is the initial term, and x_k is the last term.
There are 22 terms, the first term is 7, and the last term is 240. Hence, the sum is:
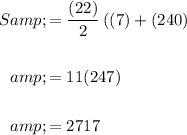
In conclusion, the sum of the arithmetic series is 2717.