The dilated triangle A ′B ′C ′ under a dilation with center P(2,2)mand a scale factor of
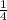 . A'
. A'
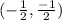 , B'
, B'
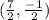 , C' (1.2, 2.55)
, C' (1.2, 2.55)
To find the new coordinates of the dilated triangle A'B'C' under a dilation with center P and a scale factor of 4, we'll use the formula I provided earlier.
Let's assume that the coordinates of the vertices of triangle ABC are as follows:
A(0,0), B(8,0), C'(4.8, 8.4)
Now, let's assume that the center of dilation is P(2, 2), and the scale factor is k =
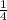
The new coordinates A', B', and C' can be calculated using the dilation formula:
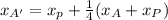
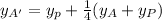
Applying this formula to each vertex:
A'= (2+
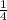 (0-2), 2 +
(0-2), 2 +
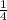 (0-2)) =
(0-2)) =
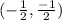
B' = (2 +
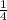 (8 - 2), 2+
(8 - 2), 2+
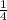 (0 - 2)) =
(0 - 2)) =
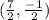
C' = (2 +
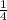 (4. 8 - 2), 2+
(4. 8 - 2), 2+
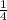 (8.4 - 2)) ≈ (1.2, 2.55)
(8.4 - 2)) ≈ (1.2, 2.55)
Now, you can plot these new coordinates on a graph to visualize the dilated triangle A ′B ′C ′.