a) Magnitudes:
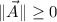 ,
,
 ,
,
 ; Directions:
; Directions:
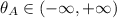 for
for
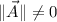 . Undefined for
. Undefined for
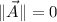 ,
,
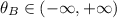 for
for
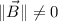 . Undefined for
. Undefined for
 ,
,
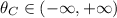 for
for
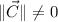 . Undefined for
. Undefined for
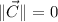 .
.
b) Magnitudes:
 ,
,
 ,
,
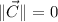 ; Directions:
; Directions:
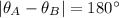 ,
,
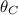 is undefined.
is undefined.
a) Let suppose that
 ,
,
 and
and
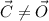 , where
, where
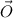 is known as Vector Zero. By definitions of Dot Product and Inverse Trigonometric Functions we derive expression for the magnitude and directions of
is known as Vector Zero. By definitions of Dot Product and Inverse Trigonometric Functions we derive expression for the magnitude and directions of
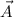 ,
,
 and
and
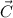 :
:
Magnitude (
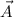 )
)
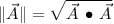
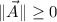
Magnitude (
 )
)
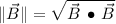

Magnitude (
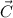 )
)
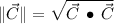

Direction (
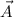 )
)
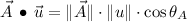

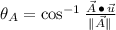
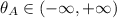 for
for
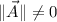 . Undefined for
. Undefined for
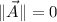 .
.
Direction (
 )
)
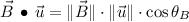
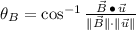
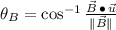
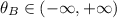 for
for
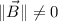 . Undefined for
. Undefined for
 .
.
Direction (
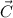 )
)
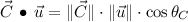

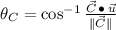
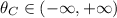 for
for
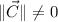 . Undefined for
. Undefined for
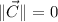 .
.
Please notice that
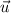 is the Vector Unit.
is the Vector Unit.
b) Let suppose that
 and
and
 and
and
 . Hence,
. Hence,
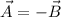 . In other words, we find that both vectors are antiparallel to each other, that is, that angle between
. In other words, we find that both vectors are antiparallel to each other, that is, that angle between
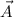 and
and
 is 180°. From a) we understand that
is 180°. From a) we understand that
 ,
,
 , but
, but
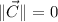 .
.
Then, we have the following conclusions:
Magnitude (
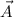 )
)

Magnitude (
 )
)

Magnitude (
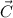 )
)
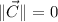
Directions (
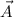 ,
,
 ):
):
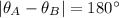
Direction (
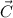 ):
):
Undefined