Explanation:
Hey there!
The given geometric sequence is: 2, -4, 8, -16.
The;
a1 = 2
Common ratio (r) = T2/T1
= -4/2
= -2
Now;
Use general formula of geometric sequence;

Where, "a1" is first term, "n" is no.of terms and "r" is common ratio.
Then;
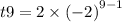
or, t9 = 2*256
Therefore, t9 = 512.
Again;
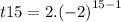
or, t15= 2*16384
Therefore, t15 = 32768.
Hope it helps!