Question

Hello! Verify the identity. Please show your work! Use trigonometric identities to verify each expression is equal.

Yes this is from edge.

Answer 1

See Below.

Explanation:

We want to verify the identity:

`\displaystyle \csc^2 x -2\csc x \cot x +\cot ^2 x = \tan^2\left((x)/(2)\right)`

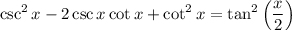
Note that the left-hand side is a perfect square trinomial pattern. Namely:

`a^2-2ab+b^2=(a-b)^2`

If we let a = csc(x) and b = cot(x), we can factor it as such:

`\displaystyle (\csc x - \cot x)^2 = \tan^2\left((x)/(2)\right)`

Let csc(x) = 1 / sin(x) and cot(x) = cos(x) / sin(x):

`\displaystyle \left((1)/(\sin x)-(\cos x )/(\sin x)\right)^2=\tan^2\left((x)/(2)\right)`

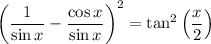
Combine fractions:

`\displaystyle \left((1-\cos x)/(\sin x)\right)^2=\tan^2\left((x)/(2)\right)`

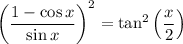
Square (but do not simplify yet):

`\displaystyle ((1-\cos x)^2)/(\sin ^2x)=\tan^2\left((x)/(2)\right)`

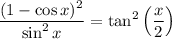
Now, we can make a substitution. Let u = x / 2. So, x = 2u. Substitute:

`\displaystyle ((1-\cos 2u)^2)/(\sin ^22u)=\tan^2u`

Recall that cos(2u) = 1 - sin²(u). Hence:

`\displaystyle ((1-(1-2\sin^2u))^2)/(\sin ^2 2u)=\tan^2u`

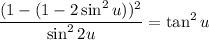
Simplify:

`\displaystyle (4\sin^4 u)/(\sin ^2 2u)=\tan^2 u`

Recall that sin(2u) = 2sin(u)cos(u). Hence:

`\displaystyle (4\sin^4 u)/((2\sin u\cos u)^2)=\tan^2 u`

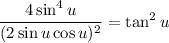
Square:

`\displaystyle (4\sin^4 u)/(4\sin^2 u\cos ^2u)=\tan^2 u`

Cancel:

`\displaystyle (\sin ^2 u)/(\cos ^2 u)=\tan ^2 u`

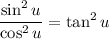
Since sin(u) / cos(u) = tan(u):

`\displaystyle \left((\sin u)/(\cos u)\right)^2=\tan^2u=\tan^2u`

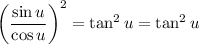
We can substitute u back for x / 2:

`\displaystyle \tan^2\left((x)/(2)\right)= \tan^2\left((x)/(2)\right)`

Hence proven.