Answer:
The magnitude of the force acting on the sled is 60.5 newtons.
Step-by-step explanation:
The Work-Energy Theorem states that the work done by the external force applied on the sled (
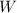 ), in joules, is equal to the change of its translational kinetic energy (
), in joules, is equal to the change of its translational kinetic energy (
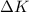 ), in joules:
), in joules:
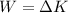 (1)
(1)
By definitions of work and translational kinetic energy we expand the equation above:
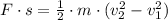 (1b)
(1b)
Where:
 - External force applied on the sled, in newtons.
- External force applied on the sled, in newtons.
 - Travelled distance, in meters.
- Travelled distance, in meters.
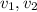 - Initial and final velocities, in meters per second.
- Initial and final velocities, in meters per second.
If we know that
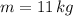 ,
,
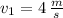 ,
,
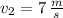 and
and
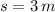 , then the external force applied on the sled is:
, then the external force applied on the sled is:
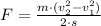
![F = ((11\,kg)\cdot \left[\left(7\,(m)/(s) \right)^(2)-\left(4\,(m)/(s) \right)^(2)\right])/(2\cdot (3\,m))](https://img.qammunity.org/2022/formulas/physics/high-school/wddepynekwcgo2qzgeuzo570m9sm1nfqma.png)
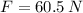
The magnitude of the force acting on the sled is 60.5 newtons.