Question

Compute the product using​ (a) the definition where Ax is the linear combination of the columns of A using the corresponding entries in x as​ weights, and​ (b) the​ row-vector rule for computing Ax. If a product is​ undefined, explain why.

Answer 1

When the number of rows or number of columns in the given matrix does not match the number of entries in the vector x.

When the number of columns in A
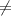`\\eq` the number of rows in B.

The matrix-vector is not defined.

Explanation:

For example:-

Step 1:

Let's assume

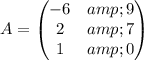`A=\left ( \begin{matrix}-6 & 9\\ 2& 7\\ 1 & 0\end{matrix} \right )`3x2 &
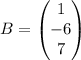`B=\left ( \begin{matrix}1\\ -6\\ 7\end{matrix} \right )`3x1

Since matrix multiplication of matric A and matrix B is only possible,

When the number of columns in A = Number of rows in B.

Step 2:

Let's A as m x n; Here m = rows and n=columns

B as p x q; Here p = rows and q=columns.

When n
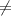`\\eq` p, the matrix-vector is not defined.

That is matrix multiplication Ax is not possible.

Hence the matrix is not defined.