A rectangle has vertices E(4,8), F(2,8), G(2,-2) and H(-4,-2). The rectangle is dilated with the origin as the center of dilation so that G's is located at (5,5). Which alg…

Question

asked Jul 18, 2022 99.5k views

1 Answer

Ivan Pianetti · Answer 1 · 2022-07-24T16:51:06+0000

Note: The image of G after the dilation must be G'(5,-5) instead of G'(5,5).

Given:

The vertices of a rectangle are E(4,8), F(2,8), G(2,-2) and H(-4,-2).

The rectangle is dilated with the origin as the center of dilation so that G's is located at (5,-5).

To find:

The algebraic representation that represents this dilation.

Solution:

If a figure is dilated by factor k with origin as the center of dilation, then the dilation is defined as:

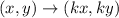$(x,y)\to (kx,ky)$ ...(i)

Let the given rectangle is dilated by factor k with origin as the center of dilation. Then,

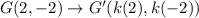
$G(2,-2)\to G'(k(2),k(-2))$

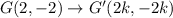
$G(2,-2)\to G'(2k,-2k)$

The image of G after dilation is G'(5,-5). So,

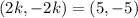
(2k,-2k)=(5,-5)

On comparing both sides, we get

2k=5

k=(5)/(2)

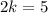
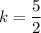
So, the scale factor is
k=(5)/(2) .

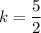Substituting
k=(5)/(2) in (i), we get

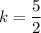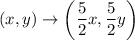
$(x,y)\to \left((5)/(2)x,(5)/(2)y\right)$

Therefore, the required algebraic representation to represents this dilation is
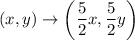$(x,y)\to \left((5)/(2)x,(5)/(2)y\right)$ .