Question

If capital rents for $25 per unit per hour, labor can be hired for $9 per unit per hour, the level of total factor productivity is normalized to 1, and the firm is minimizing costs.(a) Determine whether the production function exhibits diminishing marginal returns to each input.

Answer 1

Following are the solution to the given question:

Step-by-step explanation:

The decrease of a marginal input return implies that its input is increasing by one unit, thereby decreasing its marginal input product.

Function of production

`F(K, L) = AK^{(3)/(4)} L^{(3)/(4)}`

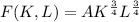
Its capital products subject (MPK) is derived by differentiating the factor of production from K.

`MPK = (3)/(4)* AK^{(3)/(4)} - 1L^{(3)/(4)}\\\\MPK = (3)/(4)AK^{-(1)/(4)}L^{(3)/(4)}\\\\MPK = (3)/(4)* A* (\frac{L^{(3)/(4)}}{K^{(1)/(4)}})`

Note: When a value is changed from numerator to denominator, then the power symbol shifts between positive to negative.

Since k is in the denominator, K decreases
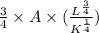`(3)/(4)* A* (\frac{L^{(3)/(4)}}{K^{(1)/(4)}})`, and therefore MPK is reduced.

There's hence a decreased effective return on capital again for production function.

Its marginal labor product (MPL) is determined by distinguishing the manufacturing function from L.

`MPL = ((3)/(4))* AK^{(3)/(4)}L^{(3)/(4)}-1\\\\MPL = ((3)/(4))AK^{(3)/(4)}L^{-(1)/(4)}\\\\MPL = ((3)/(4))* A* (\frac{K^{(3)/(4)}}{L^{(3)/(4)}})`

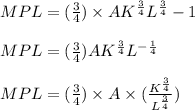
The denominator of L reduces L
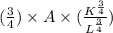`((3)/(4))* A* (\frac{K^{(3)/(4)}}{L^{(3)/(4)}})` and therefore reduces MPL.

So there is a decreasing marginal return to labor in the production function.