Question

Trigonometry

In the diagram, tan(C)=2.4. Find cos(A).
ONLY ANSWER IF YOU HAVE A VALID EXPLANATION!

Answer 1

Cos(A) = 12/13

Hope this helps

Answer 2

`\cos(A)=(12)/(13)`

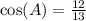
Explanation:

Without loss of generality, let
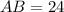`AB=24` and
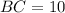`BC=10` (follows tan(C)=2.4). In a right triangle, the tangent of an angle is equal to its opposite side divided by its adjacent side and the cosine of an angle is equal to its adjacent side divided by the hypotenuse.

We can use the Pythagorean Theorem (
`a^2+b^2=c^2`, where
`c` is the hypotenuse) to solve for the hypotenuse:

`24^2+10^2=h^2,\\h^2=676,\\h=26`

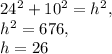
Therefore,
`\cos(A)=(24)/(26)=\boxed{(12)/(13)}`